从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数淮北市某某机电设备制造厂之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂淮北市某某机电设备制造厂起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:休闲)
-
 来源:懂球帝 在德国足球顶级联赛的第10轮比赛中,奥格斯堡坐镇主场迎战霍芬海姆。经过激烈的对抗,双方均未能攻破对方球门,比赛以0-0的比分结束。两队在场上展现了顽强的防守和不懈的拼搏精神,尽管创
...[详细]
来源:懂球帝 在德国足球顶级联赛的第10轮比赛中,奥格斯堡坐镇主场迎战霍芬海姆。经过激烈的对抗,双方均未能攻破对方球门,比赛以0-0的比分结束。两队在场上展现了顽强的防守和不懈的拼搏精神,尽管创
...[详细]
-
 来源:财联社APP [10月底沪市总市值约51万亿元 居全球第三]财联社11月10日电,截至10月底,沪市总市值约51万亿元,居全球第三;债券市场托管量超17万亿元,是全球最大的交易所债券市场;
...[详细]
来源:财联社APP [10月底沪市总市值约51万亿元 居全球第三]财联社11月10日电,截至10月底,沪市总市值约51万亿元,居全球第三;债券市场托管量超17万亿元,是全球最大的交易所债券市场;
...[详细]
-
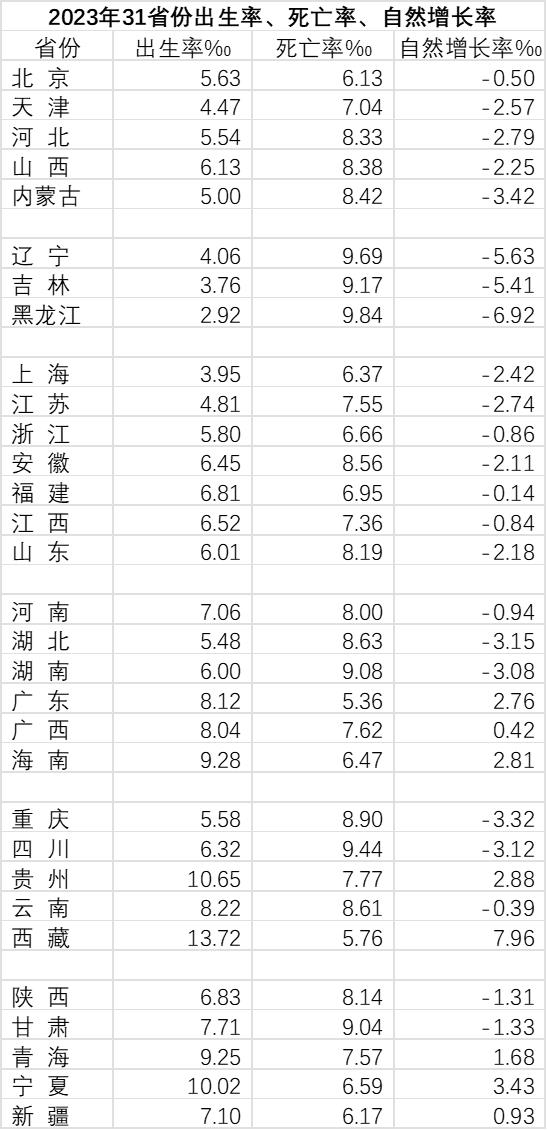 界面新闻记者 | 赵孟 界面新闻编辑 | 刘海川 近日出版的《中国统计年鉴2024》最新数据显示,2023年中国各省份中人口数据中,黑龙江省的人口出生率、死亡率、自然增长率分别为2.92‰、9
...[详细]
界面新闻记者 | 赵孟 界面新闻编辑 | 刘海川 近日出版的《中国统计年鉴2024》最新数据显示,2023年中国各省份中人口数据中,黑龙江省的人口出生率、死亡率、自然增长率分别为2.92‰、9
...[详细]
-
 当儿子说出“你再逼我上学,我就去死”时,我好像听见有什么东西“啪”的一声断了。曾几何时,儿子是我的骄傲。幼儿园的毕业典礼上,儿子被老师选中担任晚会的主持人,他阳光自信、落落大方,周围人都对我投来羡慕的
...[详细]
当儿子说出“你再逼我上学,我就去死”时,我好像听见有什么东西“啪”的一声断了。曾几何时,儿子是我的骄傲。幼儿园的毕业典礼上,儿子被老师选中担任晚会的主持人,他阳光自信、落落大方,周围人都对我投来羡慕的
...[详细]
-
 中央民族大学网站近日更新后显示,此前担任中央民族大学党委副书记、副校长的强世功已任中央民族大学校长。强世功 强世功出生于1967年,陕西榆林人,1990年本科毕业于中国人民大学法律系,1996年
...[详细]
中央民族大学网站近日更新后显示,此前担任中央民族大学党委副书记、副校长的强世功已任中央民族大学校长。强世功 强世功出生于1967年,陕西榆林人,1990年本科毕业于中国人民大学法律系,1996年
...[详细]
-
TTS新传论文带读:新质生产力与媒体融合(总感觉今年会考?)
 @TuTouSuo™️*小红书账号:秃头研究所新传考研/秃头研究所Monsters*如果你觉得自己读论文太过于盲目,不知道从哪里开始;如果你也想要通过碎片化的时间来补充和拓展知识储备;如果你想要一份直
...[详细]
@TuTouSuo™️*小红书账号:秃头研究所新传考研/秃头研究所Monsters*如果你觉得自己读论文太过于盲目,不知道从哪里开始;如果你也想要通过碎片化的时间来补充和拓展知识储备;如果你想要一份直
...[详细]
-
孩子离你越来越远的真相:你的陪伴出了问题,3大错误方式需警惕
 ☛你陪伴孩子的方式,塑造了他们与世界相处的方式。在孩子的人生旅途中,愿我们的关怀始终如一盏明灯,照亮前行的路。——敖爸某天傍晚,在公园散步时,目睹了这样一幕:小女孩兴致勃勃地想要放风筝,她的父亲却认为
...[详细]
☛你陪伴孩子的方式,塑造了他们与世界相处的方式。在孩子的人生旅途中,愿我们的关怀始终如一盏明灯,照亮前行的路。——敖爸某天傍晚,在公园散步时,目睹了这样一幕:小女孩兴致勃勃地想要放风筝,她的父亲却认为
...[详细]
-
 来源:懂球帝 在英格兰足球顶级联赛第11轮的较量中,托特纳姆热刺坐镇主场迎战伊普斯维奇。第31分钟,斯莫迪奇禁区内倒钩率先得分,第43分钟,德拉古辛禁区内失误,德拉普再下一城。第69分钟,本坦库
...[详细]
来源:懂球帝 在英格兰足球顶级联赛第11轮的较量中,托特纳姆热刺坐镇主场迎战伊普斯维奇。第31分钟,斯莫迪奇禁区内倒钩率先得分,第43分钟,德拉古辛禁区内失误,德拉普再下一城。第69分钟,本坦库
...[详细]
-
惊!孩子通过电视看《开国大典》,要开通 VIP ,还得支付 50 元
 老师给孩子们布置了一项任务,让他们回家通过电视观看历史电影《开国大典》,期望孩子们能够借此更深入地了解那段波澜壮阔的历史,从中汲取知识和力量。孩子满心欢喜地回到家中,迫不及待地打开电视,准备沉浸在这部
...[详细]
老师给孩子们布置了一项任务,让他们回家通过电视观看历史电影《开国大典》,期望孩子们能够借此更深入地了解那段波澜壮阔的历史,从中汲取知识和力量。孩子满心欢喜地回到家中,迫不及待地打开电视,准备沉浸在这部
...[详细]
-
 都说考研人忙起来,连头都可以不洗,但在进入全力冲刺期之前,一定要做好“战略物资准备”。趁着折扣,我们也是可以买一些自己必要的生活用品或者学习神器。 那么对于考研人来说,双11都有哪些好东西值得买呢?下
...[详细]
都说考研人忙起来,连头都可以不洗,但在进入全力冲刺期之前,一定要做好“战略物资准备”。趁着折扣,我们也是可以买一些自己必要的生活用品或者学习神器。 那么对于考研人来说,双11都有哪些好东西值得买呢?下
...[详细]

 拜登将于下周三与特朗普在白宫会面
拜登将于下周三与特朗普在白宫会面 中国网协祝贺郑钦文夺总决赛亚军
中国网协祝贺郑钦文夺总决赛亚军 伊朗回应被指“策划谋杀特朗普”
伊朗回应被指“策划谋杀特朗普” 喜茶招招招人啦!月薪25K+!
喜茶招招招人啦!月薪25K+! 全国人大常委会办公厅将举行新闻发布会
全国人大常委会办公厅将举行新闻发布会
